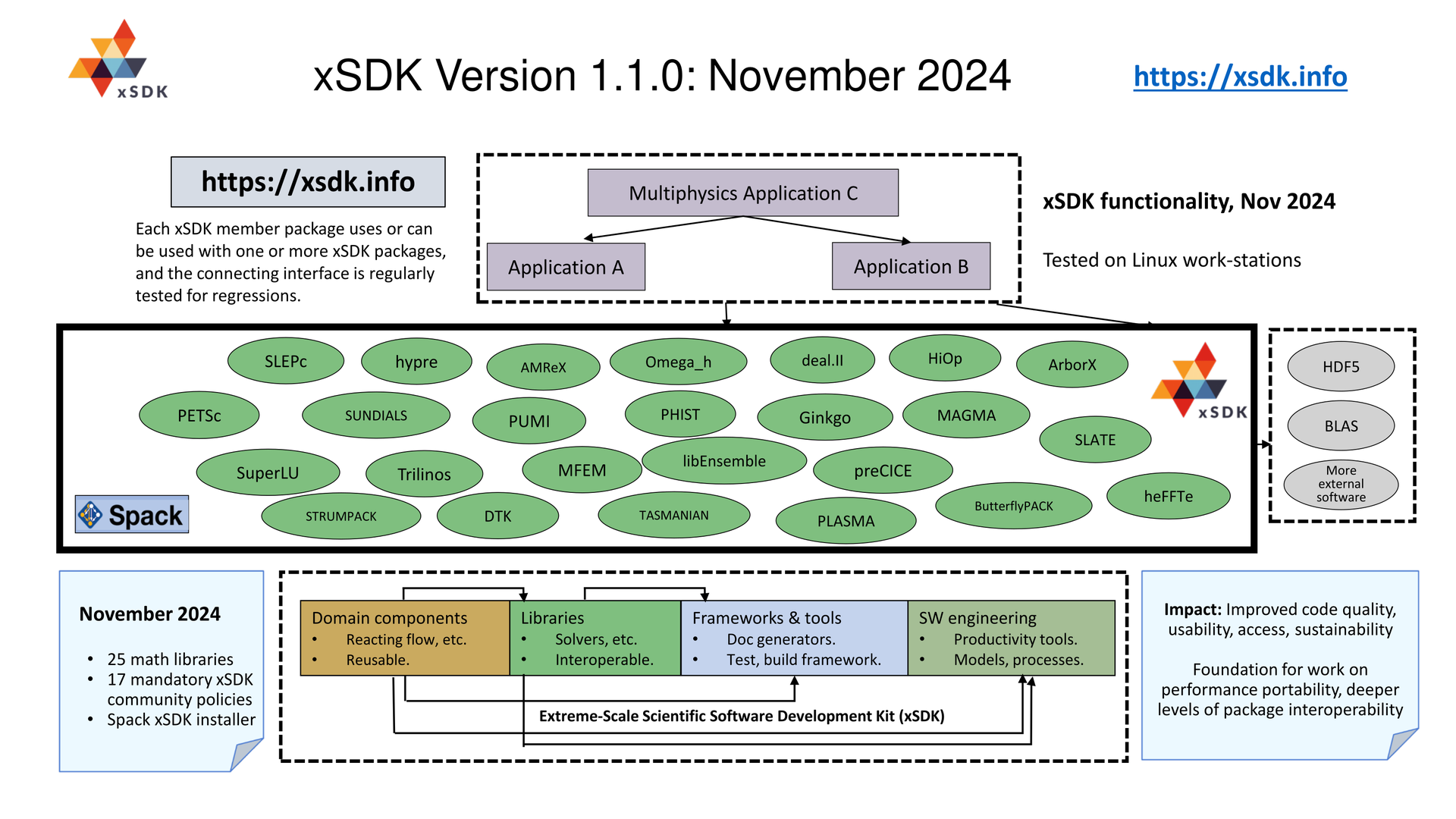
A goal of the xSDK is to improve interoperability among software libraries and domain components. The first xSDK release (xsdk-0.1.0, April 2016) comprised four widely used, independent numerical software libraries (hypre, PETSc, SuperLU, and Trilinos) and an application component (Alquimia). The second and third releases (xsdk-0.2.0-alpha, April 2017 and xsdk-0.3.0, December 2017) added the PFLOTRAN subsurface application and a few numerical libraries (MAGMA, MFEM, and SUNDIALS). The fourth release (xsdk-0.4.0, December 2018) had major additions of several scientific library packages (AMReX, deal.ii, DTK, Omega_h, PHIST, PLASMA, PUMI, SLEPc, STRUMPACK, and TASMANIAN). The fifth release (xsdk-0.5.0, November 2019) included three scientific libraries (ButterflyPACK, Ginkgo, and preCICE) and our first introduction of a python-based library (libEnsemble). The sixth release (xsdk-0.6.0, November 2020) added two numerical libraries (heFFTe, and SLATE). The seventh release (xsdk-0.7.0, November 2021) adds a geometric search library (ArborX). The eighth release (xsdk-0.8.0, November 2022) adds two numerical libraries HiOp and ExaGO. The ninth release (xsdk-1.0.0, November 2023) adds in sycl variant; additional packages are working toward compatibility with xSDK community policies and will be part of forthcoming xSDK releases. The latest release (1.1.0, November 2024) provides updated versions of current package set.
Explanations of packages’ approaches to address xSDK community policies are in the Github repo for xsdk-policy-compatibility.
We welcome the HPC community to contribute additional packages to the xSDK. See the FAQ page for information on how to contribute xSDK-compatible packages.
xSDK numerical libraries:
- AMReX
- ArborX
- ButterflyPACK
- Data Transfer Toolkit (DTK)
- deal.ii
- ExaGo
- Ginkgo
- heFFTe
- HiOp
- hypre
- libEnsemble
- MAGMA
- MFEM
- Omega_h
- PETSc/TAO
- PHIST
- PLASMA
- preCICE
- PUMI
- SLATE
- SLEPc
- STRUMPACK
- SUNDIALS
- SuperLU
- Tasmanian
- Trilinos
AMReX
AMReX is a software framework for building massively parallel block-structured AMR applications that may have particles and/or complex geometry as well as standard mesh operations. Cell-centered, face-centered and nodal mesh data are supported; there can be multiple types of particles with multiple real and/or integer attributes. Complex geometries can be represented using an embedded boundary approach, and both fluid and particle interactions with walls are enabled. Multilevel geometric multigrid solvers are included in AMReX. Parallelism is achieved using the distribution of grids to nodes using MPI as well as on-node parallelism using OpenMP, OpenACC and/or CUDA. AMReX-based applications can interface with external libraries such as CVODE, hypre, and PETSc. Highly efficient parallel I/O for checkpoint/restart and for visualization is included; AMReX’s native format is supported by tools such as Visit, Paraview, and yt. In addition, the AMReX distribution contains extensive online documentation and tutorials that demonstrate how to build parallel increasingly complex adaptive application codes using AMReX.
ArborX
ArborX is an open-source parallel geometric search library. It provides answers to questions such as: what objects are within an area of interest, or what are the closest objects to a given one. Written in C++, ArborX uses MPI and Kokkos to provide efficient, performance-portable algorithms running on a variety of platforms including the GPU accelerators (Intel, AMD, Nvidia) used in recent and upcoming supercomputers. ArborX offers a flexible C++ interface allowing you to customize the exact details of the query you want to perform, or an action to execute upon a match. In addition to the search algorithms, ArborX provides several clustering algorithms, such as DBSCAN and variants.
ButterflyPACK
ButterflyPACK is a software for rapidly solving large-scale dense linear systems that exhibit off-diagonal rank-deficiency. These systems arise frequently from boundary element methods, kernel regression, or factorization phases in finite-difference/finite-element methods. ButterflyPACK relies on low-rank and butterfly formats under Hierarchical matrix, HODLR or other hierarchically nested frameworks to compress, factor and solve the linear system in quasi-linear time. The butterfly format is a linear algebra tool well-suited for compressing matrices arising from high-frequency wave equations or highly oscillatory integral operators. ButterflyPACK can serve as a direct solver or a preconditioned iterative solver. ButterflyPACK is written in Fortran 2008, it also has C++ interfaces. In addition, ButterflyPACK has been integrated into the software STRUMPACK using the C++ interfaces for solving both dense and sparse linear systems. ButterflyPACK supports hybrid MPI/OpenMP programming models and double-precision real and complex arithmetics.
DataTransferKit (DTK)
The Data Transfer Kit (DTK) is a software library designed to provide parallel data transfer services for arbitrary physics components in large-scale, coupled simulations on heterogeneous supercomputers. DTK provides a means to geometrically correlate two geometric domains that may be arbitrarily decomposed in a parallel simulation. DTK uses portable and performant search operations to map between domains with different grids and allows for transfers between CPUs, GPUs, and combinations of both. With increased development efforts in multiphysics simulation and other multiple mesh and geometry problems, generating parallel topology maps for transferring fields and other data between geometric domains is a common operation. The algorithms used to generate parallel topology maps as implemented in DTK have been demonstrated to scale to over 100,000 MPI ranks as well as demonstrated node-local scalability on both multicore CPUs as well as the latest NVIDIA GPUs.
deal.II
deal.II is a C++ program library targeted at the computational solution of partial differential equations using finite element methods. It uses state-of-the-art programming techniques to offer a modern interface to the complex data structures and algorithms required. Its main aim is to enable rapid development of modern finite element codes, using for example h- and p-adaptive meshes, and a wide array of tools classes often used in a finite element program. deal.II supports a large number of external libraries, mainly for linear algebra operations. Applications based on deal.II have been shown to scale to over 100,000 MPI processes and reach up to 44% peak performance on recent architectures. deal.II also supports parallelism via CUDA.
ExaGO
The Exascale Grid Optimization toolkit (ExaGO) is an open source package for solving large-scale power grid nonlinear optimization problems on parallel and distributed architectures. Specifically, ExaGO can solve alternating current optimal power flow (ACOPF) problems including stochastic, contingency, and multiperiod constraints. Two optimization solvers – Ipopt and HiOp are supported for solving the optimization problems. The library is written in C/C++ using several functionalities from PETSc libraries are used for model execution on NVIDIA or AMD GPUs.
Ginkgo
With the rise of manycore accelerators like GPUs, there exists an increasing demand for linear algebra libraries that can efficiently exploit the concurrency and performance available in a single compute node and able to support the increasingly diverse range of computing technologies. At the same time, more and more application projects move towards an object-oriented software design based on C++ for both efficiency and ease of use. In the Ginkgo software effort, we design and develop a next-generation sparse linear algebra library able to run on multi- and manycore architectures. The library design is guided by combining ecosystem extensibility with heavy, architecture-specific kernel optimization using the platform-native languages CUDA (NVIDIA GPUs), HIP (AMD GPUs), or OpenMP (Intel/AMD multicore). The software development cycle ensures production-quality code by featuring unit testing, automated configuration and installation, Doxygen code documentation, as well as a continuous integration and continuous benchmarking framework. Ginkgo is an open source effort licensed under BSD 3-clause.
heFFTe
The Highly Efficient FFTs for Exascale( heFFTe) library provides fast and robust multidimensional Fast Fourier transforms (FFTs) for large-scale heterogeneous systems with multi-core processors and hardware accelerators, and is codesigned with ECP application developers. FFTs are used in applications ranging from molecular dynamics and spectrum estimation to machine learning, fast convolution and correlation, signal modulation, wireless multimedia applications, and others, including more than a dozen ECP applications. HeFFTe collects and leverages existing FFT capabilities while building a sustainable FFT library that minimizes data movements, optimizes MPI communications, overlaps computations with communications, and autotunes performance on various architectures andlarge scale platforms. HeFFTe targets Exascale platforms, currently achieving very good scalability on pre-exascale systems, and a performance that is close to 90% of the roofline peak.
HiOp
The High-performance Optimization (HiOp) library is a suite of optimization solvers capable of portable high-performance computing. HiOp provides first-order methods (such as limited-memory quasi-Newton and bundle methods) and second-order methods (such as nonconvex filter line-search interior point methods) for solving general nonlinear nonconvex mathematical optimization problems. Depending on the problem structure, HiOp can achieve coarse-grain (i.e., MPI-based, internode) and/or fine-grain (e.g., for hardware accelerators) parallelism by using a combination of specialized, problem-specific decomposition schemes and linear algebra kernels running on accelerators. HiOp achieves portability mainly by using RAJA, Umpire, MAGMA, and Ginkgo libraries, but performance-critical kernels for Nvidia and AMD accelerators are implemented using low-level hardware-specific code or vendor-specific API. Among the current uses of HiOp, we mention the exaGO optimization power grid library, LiDO structural design optimization code, mesh optimization in MFEM, and contact mechanics at LLNL.
hypre
Hypre provides high-performance preconditioners and solvers for the solution of large, sparse linear systems on massively parallel computers, with focus on algebraic multigrid methods. It was created with the primary goal of providing users with advanced parallel preconditioners. For ease of use, these solvers are accessed from the application code via hypre’s conceptual linear system interfaces, which allow a variety of natural problem descriptions and include a structured, a semi-structured interface, and a traditional linear-algebra based interface. The (semi-)structured interfaces are an alternative to the standard matrix-based interface, give users a more natural means for describing linear systems and provide access to structured multigrid solvers, which can take advantage of the additional information. Hypre can be used with MPI and OpenMP and has support for NVIDIA, AMD and Intel GPUs.
libEnsemble
libEnsemble is a Python library to coordinate the concurrent evaluation of dynamic ensembles of calculations. The library is developed to use massively parallel resources to accelerate the solution of design, decision, and inference problems and to expand the class of problems that can benefit from increased concurrency levels. libEnsemble uses a manager-worker paradigm and supplies a portable interface for users to launch and monitor jobs via simulation and generation routines; this interface facilitates resource detection, built-in resilience to failures, selective job termination, and resource recovery. To work effectively in diverse scenarios, MPI-, multiprocessing-, and TCP-based communication layers are provided; interfacing with user-provided executables is also supported. Example simulation and generation functions are available and include sensitivity analysis, numerical optimization, and statistical calibration.
MAGMA
MAGMA is a dense linear algebra library that implements LAPACK functionality for heterogeneous platforms that feature GPUs. MAGMA addresses the complex challenges of such hybrid environments with hybridized software that combines the strengths of different algorithms within a single framework. MAGMA’s linear algebra algorithms target hybrid manycore systems featuring GPUs specifically and thus enable applications to fully exploit the power offered by each of the hardware components. MAGMA provides solvers for linear systems, least squares problems, eigenvalue problems, and singular value problems. Designed to be similar to LAPACK in functionality, data storage, and interface, the MAGMA library allows scientists to easily port their existing software components from LAPACK to MAGMA, to take advantage of new hybrid architectures. Also included is MAGMA BLAS, a complementary to CUBLAS routines.
MFEM
MFEM is a lightweight, scalable C++ library for finite element discretizations of partial differential equations on unstructured grids, with emphasis on high-order methods and applications. It has a number of unique features, including: support for arbitrary order finite element meshes and spaces with both conforming and nonconforming adaptive mesh refinement; advanced finite element spaces and discretizations, such as mixed methods, DG (discontinuous Galerkin), DPG (discontinuous Petrov-Galerkin) and Isogeometric Analysis (IGA) on NURBS (Non-Uniform Rational B-Splines) meshes; native support for the high-performance Algebraic Multigrid (AMG) preconditioners from the hypre library; integration with many other math libraries, including PETSc, SUNDIALS and SuperLU; and a large number of well-documented example codes and miniapps.
Omega_h
Omega_h is a C++ library providing a parallel mesh data structure and algorithms for parallel mesh adaptation. The mesh adaptation methods implemented in Omega_h represent the state of the art for anisotropic metric-based adaptation of all-triangle and all-tetrahedron meshes. It can be used to add advanced adaptive capabilities to existing simulation codes, or even as the fundamental mesh structure for such simulation codes. Omega_h has scalable MPI parallelism up to billions of elements on tens of thousands of cores. It also has very mature on-node parallelism using OpenMP or CUDA, with very good GPU performance of complex operations such as mesh adaptation. In order to support this, it provides a variety of basic utilities including small local linear algebra (dozens of unknowns or less) which executes efficiently on GPUs.
PETSc/TAO
PETSc is a suite of data structures and routines for the scalable solution of scientific applications modeled by partial differential equations, while TAO is a scalable optimization library. The software includes linear solvers, preconditioners, nonlinear solvers, and ODE integrators, as well as a variety of scalable constrained and unconstrained optimization solvers. PETSc uses MPI for distributed memory parallelism and supports NVIDIA, AMD and Intel GPUs and interfaces to them via Kokkos. It can be used with and without GPU-aware MPI . While PETSc does not include eigensolvers, the eigensolver package SLEPc, built on top of PETSc, has a very similar interface. The library libMesh and the framework MOOSE provide finite element solvers that utilize PETSc. PETSc/TAO can be easily used in application codes written in C, C++, Fortran, and Python.
PHIST
PHIST addresses the iterative solution of sparse linear and eigenvalue problems. It introduces an abstraction layer by which applications can construct and solve sparse problems independent of the underlying implementation and hardware. The interface is available in C, C++, Fortran’03 and Python. Supported backends include Trilinos (Epetra/Tpetra), PETSc and Eigen, but there are also highly optimized MPI+OpenMP kernels for multi-/manycore CPUs included, and via GHOST we support heterogeneous parallelism using MPI, OpenMP and CUDA. Within the xSDK, PHIST uses Tpetra. PHIST’s flagship eigensolver is the block Jacobi-Davidson QR method for non-Hermitian and/or generalized eigenvalue problems. It exploits kernel fusion and blocking for increased performance and can exploit preconditioners. With the Tpetra backend we support MueLU (AMG preconditioners) and Ifpack2 (incomplete factorizations). Common iterative linear solvers like CG, GMRES, and BiCGStab are available in blocked versions that solve for multiple right-hand sides and with different diagonal shifts if desired.
PLASMA
PLASMA is a software package for solving problems in dense linear algebra using multicore and many-core processors. PLASMA provides implementations of state-of-the-art algorithms using cutting-edge task scheduling techniques. PLASMA provides routines for solving linear systems, least squares problems, eigenvalue problems, and singular value problems. PLASMA is based on OpenMP and its data-dependence tracking and task scheduling. PLASMA library allows scientists to easily port their existing software components from LAPACK to PLASMA to take advantage of the new multicore architectures. PLASMA provides LAPACK-style interface for maximum portability and compatibility. An interface with more efficient data storage is also provided to achieve performance as close as possible to the computational peak performance of the machine.
preCICE
preCICE (Precise Code Interaction Coupling Environment) is a coupling library for partitioned multi-physics simulations, including, but not restricted to fluid-structure interaction and conjugate heat transfer simulations. Partitioned means that preCICE couples existing programs (solvers) capable of simulating a subpart of the complete physics involved in a simulation. This allows for the high flexibility that is needed to keep a decent time-to-solution for complex multi-physics scenarios. preCICE runs efficiently on a wide spectrum of systems, from low-end workstations up to complete compute clusters and has proven scalability on 10,000s of MPI Ranks. The software offers methods for transient equation coupling, communication means, and data mapping schemes. preCICE is written in C++ and offers bindings for C, Fortran, Matlab, and Python. Ready-to-use adapters for well-known commercial and open-source solvers, such as OpenFOAM, deal.II, FEniCS, SU2, or CalculiX, are available.
PUMI
An efficient distributed mesh data structure is needed to support parallel adaptive analysis since it strongly influences the overall performance of adaptive mesh-based simulations. In addition to the general mesh-based operations, such as mesh entity creation/deletion, adjacency and geometric classification, iterators, arbitrary attachable data to mesh entities, etc., the distributed mesh data structure must support (i) efficient communication between entities duplicated over multiple processors, (ii) migration of mesh entities between processors, and (iii) dynamic load balancing. Issues associated with supporting parallel adaptive analysis on unstructured meshes include dynamic mesh load balancing techniques, and data structure and algorithms for parallel mesh adaptation. The Parallel Unstructured Mesh Infrastructure (PUMI) is an unstructured, distributed mesh data management system that is capable of handling general non-manifold models and effectively supporting automated adaptive analysis.
SLATE
SLATE is a C++ library for distributed, GPU-accelerated, dense linear algebra covering existing LAPACK and ScaLAPACK functionality, including parallel implementations of Basic Linear Algebra Subroutines (BLAS), linear systems solvers (LU, Cholesky, symmetric indefinite), least squares solvers (QR and LQ), eigenvalue solvers, and the singular value decomposition (SVD). SLATE offers a modern C++ interface with matrix classes and functions templated on precision (e.g., single or double, real or complex). It also provides a backwards-compatibility API for ScaLAPACK and LAPACK, to ease the transition from legacy APIs. The BLAS++ and LAPACK++ libraries providing C++ wrappers around traditional Fortran BLAS/LAPACK and GPU BLAS (e.g., cuBLAS) are also developed as part of the SLATE project.
SLEPc
SLEPc is a library for the parallel computation of eigenvalues and eigenvectors of large, sparse matrices. It relies on PETSc and complements it by providing solvers for different types of eigenproblems, including linear (standard and generalized) and nonlinear (quadratic, polynomial and general), as well as the SVD (singular values and vectors). In addition to eigenvalue problems, SLEPc also provides functionality related to matrix functions, in particular it can compute the action of a function (such as the exponential or the square root) of a matrix on a vector. SLEPc uses the MPI standard for parallelization, but it also has support for GPUs. With SLEPc, the application programmer can use any of PETSc’s data structures and solvers. Other PETSc features are incorporated into SLEPc as well, such as command-line option setting, automatic profiling, error checking, portability, etc.
STRUMPACK
STRUMPACK (STRUctured Matrix PACKage) is a software library providing linear algebra routines for sparse matrices and for dense rank-structured matrices, i.e., matrices that exhibit some kind of low-rank property. STRUMPACK aims to support a variety of hierarchical matrix formats, such as Hierarchically Semi-Separable (HSS) and Hierarchically Off-Diagonal Low Rank (HODLR). These appear in many applications, e.g., Finite Element Methods, Boundary Element Methods, etc. STRUMPACK provides distributed memory dense matrix algorithms and a distributed memory fully algebraic sparse general solver and preconditioner. The preconditioner is mostly aimed at large sparse linear systems which result from the discretization of a partial differential equation, but is not limited to any particular type of problem. STRUMPACK also provides preconditioned GMRES and BiCGStab iterative solvers.
SUNDIALS
SUNDIALS is a SUite of Nonlinear and DIfferential/ALgebraic equation Solvers and integrators. It consists of six packages: CVODE solves initial value problems for ordinary differential equation (ODE) systems using variable order and step linear multistep methods; CVODES solves ODE systems and includes sensitivity analysis capabilities (forward and adjoint); ARKODE solves initial value ODE problems with variable step Runge-Kutta methods, including support for explicit, implicit, and additive implicit/explicit (IMEX) integration methods; IDA solves initial value problems for differential-algebraic equation (DAE) systems using variable order and step linear multistep methods; IDAS solves DAE systems and includes sensitivity analysis capabilities (forward and adjoint); and KINSOL solves nonlinear algebraic systems with both Newton-based and fixed point iterative methods. SUNDIALS is written in C and is supplied with iterative and direct linear solvers. Parallelism is fully encapsulated in the data vector API. Users can supply their own vectors or employ SUNDIALS-supplied vectors using distributed memory (via MPI), shared memory (via openMP and PThreads), or GPU-based (via CUDA or RAJA) parallelism.
SuperLU
SuperLU is a general-purpose library for the direct solution of large, sparse, nonsymmetric systems of linear equations on high-performance machines. The library routines will perform an LU decomposition with partial pivoting and triangular system solves through forward and back substitution. The LU factorization routines can handle non-square matrices, but the triangular solves are performed only for square matrices. The matrix columns may be preordered (before factorization) either through library or user supplied routines. This preordering for sparsity is completely separate from the factorization. Working precision iterative refinement subroutines are provided for improved backward stability. Routines are also provided to equilibrate the system, estimate the condition number, calculate the relative backward error, and estimate error bounds for the refined solutions. There are three separate versions of this code: SuperLU (for sequential machines), SuperLU_MT (for shared memory parallel machines with using OpenMP or Pthread), and SuperLU_DIST (for distributed memory machines using MPI). The library is written in C, with a Fortran interface. SuperLU_DIST supports MPI+X, where X can be CUDA, OpenMP, or both.
TASMANIAN
The Toolkit for Adaptive Stochastic Modeling And Non-Intrusive ApproximatioN is a collection of robust libraries for high dimensional integration and interpolation as well as parameter calibration. The code consists of several modules that can be used individually or conjointly. Tasmanian implements a wide range of Sparse Grid methods based on polynomials with global or local support, wavelet and trigonometric (periodic) functions; the methods focus on surrogate modeling with applications of uncertainty quantification. In addition, Tasmanian implements the DiffeRential Evolution Adaptive Metropolis (DREAM) algorithm for generating random samples from an arbitrary (non-separable) probability distribution; DREAM is often used to sample posterior distributions in the context of Bayesian inference and model validation and calibration.
Trilinos
The Trilinos Project is an effort to develop algorithms and enabling technologies within an object-oriented software framework for the solution of large-scale, complex multiphysics engineering and scientific problems. Trillions is organized into 66 different packages, each with a specific focus. These packages include linear and nonlinear solvers, preconditioners (including algebraic multigrid), graph partitioners, eigensolvers, and optimization algorithms, among other things. Users are required to install only the subset of packages related to the problems they are trying to solve. Trilinos supports MPI+X, where X can be CUDA, OpenMP, etc.
xSDK application packages:
Alquimia
Alquimia provides an API for exposing mature geochemistry and biogeochemistry capabilities to reactive transport codes. Alquimia is not a geochemistry solver; rather, it is a library comprising data structures and interfaces that wrap chemistry solvers from well-established codes like PFLOTRAN and CrunchFlow, thereby allowing developers of new codes to use these solvers with a single interface. We refer to these chemistry solvers as chemistry engines.
PFLOTRAN
PFLOTRAN is an open source, massively parallel subsurface flow and reactive transport code. PFLOTRAN solves a system of generally nonlinear partial differential equations describing multiphase, multicomponent and multiscale reactive flow and transport in porous materials. Parallelization is achieved through domain decomposition using the PETSc. The reactive transport equations can be solved using either a fully implicit Newton-Raphson algorithm or the less robust operator splitting method.