xSDK tutorials

• An introduction to the xSDK, a community of diverse numerical HPC software packages [slides in pdf], tutorial presented at the 2019 ECP Annual Meeting, January 15, 2019

Simple xSDK example application

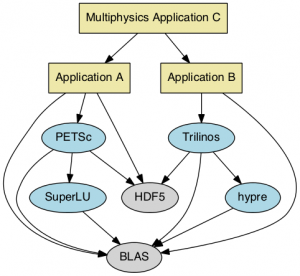
This diagram illustrates a new multiphysics application C, built from two complementary applications that employ four xSDK packages (shown in blue): Application A uses PETSc for an implicit-explicit time advance, which in turn interfaces to SuperLU to solve the resulting linear systems.  Application B uses Trilinos to solve a nonlinear system, which in turn interfaces to hypre to solve the resulting linear systems. This work has enabled a single-executable build of application C as a first step toward broader support for xSDK library interoperability, so that scientific applications can be easily constructed to use the full features of multiple complementary packages.  A more general diagram of xSDK functionality is here.

As part of linking together the entire application, it is crucial that the compilation system ensure that a single BLAS (or HDF5 or other external) library be shared by all packages rather than having multiple, incompatible versions in the executable, which would lead to mysterious crashes or incorrect results. As part of our xSDK work, we are making it easy to ensure such correct linking.  The xSDK package interactions for use-cases in subsurface simulation are more complex than represented by this simple diagram and include interoperability among all four initial xSDK numerical libraries; see the diagram in the section “Impact on Scientific Applications” on the xSDK home page.

Getting started guides, emphasizing xSDK package interoperability

As illustrated by the above diagram, the current release of xSDK provides linear solver interoperability, so that both PETSc and Trilinos can call linear solvers from each other as well as from hypre and SuperLU.  Because the specific solver challenges for applications vary according to particular models and simulations, easy access to a diverse suite of linear solvers is essential in order to achieve robust, efficient, and scalable performance.  Below we provide details about how application codes can employ this xSDK interoperability layer to easily access different scalable solvers as dictated by the needs of application codes.

Getting started with xSDK/PETSc:

PETSc approach to package interoperability. PETSc is an object-oriented library, where each abstract base class (for example, the abstract base matrix class Mat) defines a set of interfaces (for example, the matrix-vector product). The concrete classes are implemented via delegation; that is, method calls on the object (Mat) are passed to an inner implementation-specific object (for example Mat_SeqAIJ) that actually provides the code for the operation. This allows the selection of the specific concrete class used to be delayed until runtime, without the need for factory objects and for the implementation class to be changed (from perhaps SeqAIJ to matrix-free) in the middle of a simulation without needing to recreate any objects. This model makes basic interoperability with other object-oriented (hypre, Trilinos) or object-based (SuperLU) libraries straightforward. One simply provides a wrapper object that exposes the PETSc object interface and translates the calls to the interface of the other package.  We currently have preconditioner class wrappers for hypre and the ML package of Trilinos, factored matrix class wrappers for SuperLU/SuperLU_DIST, and partitioner class wrappers for the Zoltan package of Trilinos. PETSc also has dozens of other class wrappers for other HPC packages. Details of the PETSc implementation of classes via delegation can be found in the PETSc developers manual.

Hands-on examples that demonstrate use of xSDK algebraic solvers across packages:

• PETSc interoperability with hypre
• PETSc interoperability with SuperLU
• PETSc interoperability with Trilinos

Getting started with xSDK/Trilinos: 

xSDKTrilinos is a package that facilitates interoperability of Trilinos with other xSDK packages, specifically linear solvers in hypre, PETSc, and SuperLU.  The xSDKTrilinos User Manual explains details about the approach and provides examples that demonstrate use of algebraic solvers across packages:

• Trilinos interoperability with hypre
• Trilinos interoperability with PETSc
• Trilinos interoperability with SuperLU

Example codes suite demonstrating xSDK package interoperability 

Achieving and maintaining interoperability between xSDK libraries is an important goal of the xSDK project. To aid understanding of how to use these capabilities, a suite of example codes has been provided. The suite currently provides examples showing the following interoperabilities (‘lib1 + lib2‘ indicates that lib1 calls lib2):

The examples can be installed along with the xSDK utilizing the Spack package.

spack install xsdk-examples

To install with CUDA support,

spack install xsdk-examples+cuda cuda_arch=<arch>

Since xsdk-examples depends on the xsdk Spack package, Spack will also install xsdk. In many cases, it may be easier to install the xsdk package (separately) following https://xsdk.info/download/ prior to the xsdk-examples package.

Alternatively, the examples can be built and installed with CMake:

git clone https://github.com/xsdk-project/xsdk-examples
cmake -DCMAKE_PREFIX_PATH=/path/to/libraries -DENABLE_CUDA=<TRUE|FALSE> -DENABLE_HIP=<TRUE|FALSE> -S xsdk-examples/ -B xsdk-examples/builddir
cd xsdk-examples/builddir
make
make install

Note, that to build with HIP support it is recommended to use CMake directly.

Descriptions of the example problems and instructions on how to run the executables are available in the README files located in the subdirectories containing the source codes.